Advertisements
Advertisements
प्रश्न
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
उत्तर
A is the position of the 1st train.
B is the position of the 2nd train.
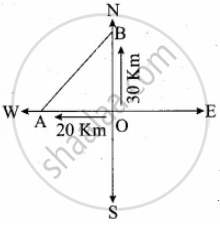
Distance Covered in 2 hours
OA = 2 × 20 = 40 km
OB = 2 × 30 = 60 km
Distance between the train after 2 hours
AB = `sqrt("OA"^2 + "OB"^2)`
= `sqrt(40^2 + 60^2)`
= `sqrt(1600 + 3600)`
= `sqrt(5200)` or `sqrt(52 xx 100)`
= `10sqrt(4 xx 13)`
= `20sqrt(13)`
= 72.11 km
Distance between the two train = 72.11 km or `20sqrt(13) "km"`
APPEARS IN
संबंधित प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
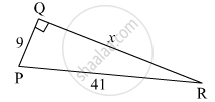
In the figure below, find the value of 'x'.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
The longest side of a right angled triangle is called its ______.
