Advertisements
Advertisements
प्रश्न
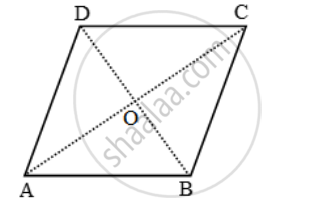
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
उत्तर १
Let the diagonals AC and BD of rhombus ABCD intersect at O.
Since the diagonals of a rhombus bisect each other at right angles.
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90º and AO = CO, BO = OD.
Since ∆AOB is a right triangle right-angle at O.
∴ AB2 = OA2 + OB2
`AB^2=(1/2AC)^2 +(1/2BD)^2 `
⇒ 4AB2 = AC2 + BD2 ….(i)
Similarly, we have
`4BC^2 = AC^2 + BD^2 ….(ii)`
`4CD^2 = AC^2 + BD^2 ….(iii)`
and,
`4AD^2 = AC^2 + BD^2 ….(iv)`
Adding all these results, we get
`4(AB^2 + BC^2 + AD^2 ) = 4(AC^2 + BD^2 )`
`⇒ AB^2 + BC^2 + AD^2 + DA^2 = AC^2 + BD^2`
उत्तर २

In ΔAOB, ΔBOC, ΔCOD, ΔAOD
Applying Pythagoras theorem
AB2 = AO2 + OB2
BC2 = BO2 + OC2
CD2 = CO2 + OD2
AD2 = AO2 + OD2
Adding all these equations,
AB2 + BC2 + CD2 + AD2
= 2(AO2 + OB2 + OC2 + OD2)
= `2{("AC"/2)^2 + ("BD"/2)^2 + ("AC"/2)^2 + ("BD"/2)^2}` ...(diagonals bisect each other)
= `2(("AC")^2/2 + ("BD")^2/2)`
= (AC)2 + (BD)2
APPEARS IN
संबंधित प्रश्न
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.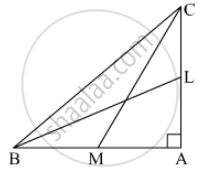
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
