Advertisements
Advertisements
Question
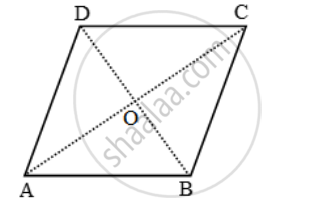
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
Solution 1
Let the diagonals AC and BD of rhombus ABCD intersect at O.
Since the diagonals of a rhombus bisect each other at right angles.
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90º and AO = CO, BO = OD.
Since ∆AOB is a right triangle right-angle at O.
∴ AB2 = OA2 + OB2
`AB^2=(1/2AC)^2 +(1/2BD)^2 `
⇒ 4AB2 = AC2 + BD2 ….(i)
Similarly, we have
`4BC^2 = AC^2 + BD^2 ….(ii)`
`4CD^2 = AC^2 + BD^2 ….(iii)`
and,
`4AD^2 = AC^2 + BD^2 ….(iv)`
Adding all these results, we get
`4(AB^2 + BC^2 + AD^2 ) = 4(AC^2 + BD^2 )`
`⇒ AB^2 + BC^2 + AD^2 + DA^2 = AC^2 + BD^2`
Solution 2

In ΔAOB, ΔBOC, ΔCOD, ΔAOD
Applying Pythagoras theorem
AB2 = AO2 + OB2
BC2 = BO2 + OC2
CD2 = CO2 + OD2
AD2 = AO2 + OD2
Adding all these equations,
AB2 + BC2 + CD2 + AD2
= 2(AO2 + OB2 + OC2 + OD2)
= `2{("AC"/2)^2 + ("BD"/2)^2 + ("AC"/2)^2 + ("BD"/2)^2}` ...(diagonals bisect each other)
= `2(("AC")^2/2 + ("BD")^2/2)`
= (AC)2 + (BD)2
APPEARS IN
RELATED QUESTIONS
If the sides of a triangle are 6 cm, 8 cm and 10 cm, respectively, then determine whether the triangle is a right angle triangle or not.
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
Find the unknown side in the following triangles
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
