Question

Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.

Answer 1

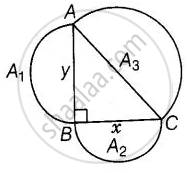
Let ABC be a right triangle, right angled at B and AB = y, BC = x.

Three semi-circles are drawn on the sides AB, BC and AC, respectively with diameters AB, BC and AC, respectively.

Again, let area of circles with diameters AB, BC and AC are respectively A₁, A₂ and A₃.

To prove: A₃ = A₁ + A₂

Proof: In ΔABC,

By pythagoras theorem,

AC² = AB² + BC²

⇒ AC² = y² + x²

⇒ AC = `sqrt(y^2 + x^2)`

We know that,

Area of a semi-circle with radius,

r = `(pir^2)/2`

∴ Area of semi-circle drawn on AC,

A₃ = `pi/2(("AC")/2)^2`

= `pi/2(sqrt(y^2 + x^2)/2)^2`

⇒ A₃ = `(pi(y^2 + x^2))/8`  ...(i)

Now, area of semi-circle drawn on AB,

A₁ = `pi/2 (("AB")/2)^2`

⇒ A₁ = `pi/2(y/2)^2`

⇒ A₁ = `(piy^2)/8`  ...(ii)

And area of semi-circle drawn on BC,

A₂ = `pi/2(("BC")/2)^2`

= `pi/2(x/2)^2`

⇒ A₂ = `(pix^2)/8`

On adding equations (ii) and (iii), we get

A₁ + A₂ = `(piy^2)/8 + (pix^2)/8`

= `(pi(y^2 + x^2))/8`

= A₃   ...[From equation (i)]

⇒ A₁ + A₂ = A₃

Hence proved.