Advertisements
Online Mock Tests
Chapters
2: Polynomials
3: Pair of Liner Equation in Two Variable
4: Quadatric Euation
5: Arithematic Progressions
▶ 6: Triangles
7: Coordinate Geometry
8: Introduction To Trigonometry and Its Applications
9: Circles
10: Construction
11: Area Related To Circles
12: Surface Areas and Volumes
13: Statistics and Probability
![NCERT Exemplar solutions for Mathematics [English] Class 10 chapter 6 - Triangles NCERT Exemplar solutions for Mathematics [English] Class 10 chapter 6 - Triangles - Shaalaa.com](/images/mathematics-english-class-10_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 6: Triangles
Below listed, you can find solutions for Chapter 6 of CBSE NCERT Exemplar for Mathematics [English] Class 10.
NCERT Exemplar solutions for Mathematics [English] Class 10 6 Triangles Exercise 6.1 [Pages 60 - 62]
Choose the correct alternative:
In Figure, ∠BAC = 90° and AD ⊥ BC. Then, ______.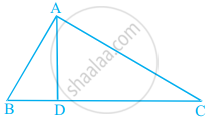
BD . CD = BC2
AB . AC = BC2
BD . CD = AD2
AB . AC = AD2
The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is ______.
9 cm
10 cm
8 cm
20 cm
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
BC . EF = AC . FD
AB . EF = AC . DE
BC . DE = AB . EF
BC . DE = AB . FD
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
ΔPQR ~ ΔCAB
ΔPQR ~ ΔABC
ΔCBA ~ ΔPQR
ΔBCA ~ ΔPQR
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
50°
30°
60°
100°
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
`("EF")/("PR") = ("DF")/("PQ")`
`("DE")/("PQ") = ("EF")/("RP")`
`("DE")/("QR") = ("DF")/("PQ")`
`("EF")/("RP") = ("DE")/("QR")`
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
congruent but not similar
similar but not congruent
neither congruent nor similar
congruent as well as similar
It is given that ΔABC ~ ΔPQR, with `(BC)/(QR) = 1/3`. Then, `(ar(PRQ))/(ar(BCA))` is equal to ______.
9
3
`1/3`
`1/9`
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
DE = 12 cm, ∠F = 50°
DE = 12 cm, ∠F = 100°
EF = 12 cm, ∠D = 100°
EF = 12 cm, ∠D = 30°
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
∠B = ∠E
∠A = ∠D
∠B = ∠D
∠A = ∠F
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
10 cm
12 cm
`20/3` cm
8 cm
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
PR . QR = RS2
QS2 + RS2 = QR2
PR2 + QR2 = PQ2
PS2 + RS2 = PR2
NCERT Exemplar solutions for Mathematics [English] Class 10 6 Triangles Exercise 6.2 [Pages 63 - 65]
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?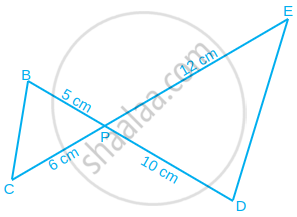
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
True
False
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
The ratio of the corresponding altitudes of two similar triangles is `3/5`. Is it correct to say that ratio of their areas is `6/5`? Why?
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?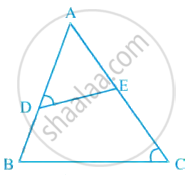
Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer.
NCERT Exemplar solutions for Mathematics [English] Class 10 6 Triangles Exercise 6.3 [Pages 66 - 69]
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
Find the value of x for which DE || AB in figure.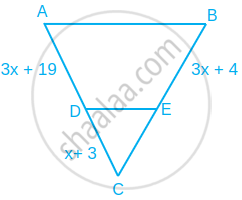
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
Find the altitude of an equilateral triangle of side 8 cm.
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).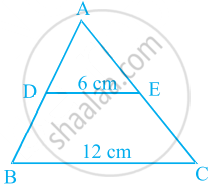
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.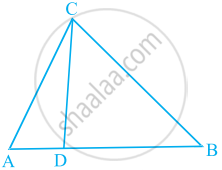
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
NCERT Exemplar solutions for Mathematics [English] Class 10 6 Triangles Exercise 6.4 [Pages 73 - 76]
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.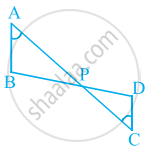
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
In figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
In figure, ABC is a triangle right angled at B and BD ⊥ AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.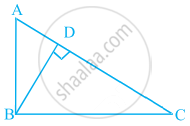
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Solutions for 6: Triangles
![NCERT Exemplar solutions for Mathematics [English] Class 10 chapter 6 - Triangles NCERT Exemplar solutions for Mathematics [English] Class 10 chapter 6 - Triangles - Shaalaa.com](/images/mathematics-english-class-10_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 10 chapter 6 - Triangles
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 10 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 10 CBSE 6 (Triangles) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 10 chapter 6 Triangles are Similar Figures, Similarity of Triangles, Basic Proportionality Theorem (Thales Theorem), Criteria for Similarity of Triangles, Areas of Similar Triangles, Triangles Examples and Solutions, Right-angled Triangles and Pythagoras Property, Similarity of Triangles, Similarity of Triangles, Application of Pythagoras Theorem in Acute Angle and Obtuse Angle, Ratio of Sides of Triangle, Concept of Angle Bisector.
Using NCERT Exemplar Mathematics [English] Class 10 solutions Triangles exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 10 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 6, Triangles Mathematics [English] Class 10 additional questions for Mathematics Mathematics [English] Class 10 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
