Advertisements
Advertisements
Question
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.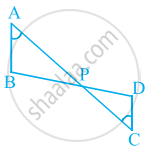
Solution
According to the question,
∠A = ∠C,
AB = 6 cm,
BP = 15 cm,
AP = 12 cm
CP = 4 cm
From ∆APB and ∆CPD,
∠A = ∠C
∠APB = ∠CPD ...[Vertically opposite angles]
∴ By AAA similarity criteria,
ΔAPD ∼ ΔCPD
Using basic proportionality theorem,
⇒ `("AP")/("CP") = ("PB")/("PD") = ("AB")/("CD")` ...[By basic proportionality theorem]
⇒ `12/4 = 15/("PD") = 6/("CD")`
Considering `("AP")/("CP") = ("PB")/("PD")`, we get,
`12/4 = 15/("PD")`
PD = `(15 xx 4)/12`
= `60/12`
= 5 cm
Considering, `("AP")/("CP") = ("AB")/("CD")`
⇒ CD = `((6 xx 4))/12` = 2 cm
Therefore,
Length of PD = 5 cm
Length of CD = 2 cm
APPEARS IN
RELATED QUESTIONS
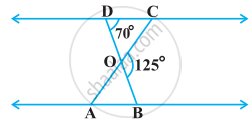
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB) = 84cm2. Find ar(ΔCOD).
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

