Advertisements
Advertisements
Question
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
Solution
When two triangles are similar, then the ratios of the lengths of their corresponding sides are equal.
Here, ΔABC ~ΔDEF
∴ `(AB)/(DE)=(BC)/(EF)`
⇒`( AB)/(2AB)=(6)/(EF)`
⇒ EF = 12 cm
APPEARS IN
RELATED QUESTIONS
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
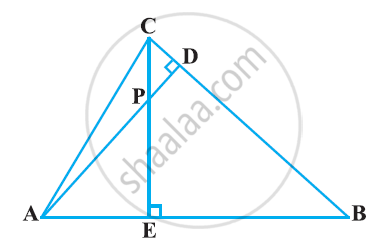
ΔAEP ∼ ΔADB
In the following figure, AB || QR. Find the length of PB.

In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
State the AAA-similarity criterion
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?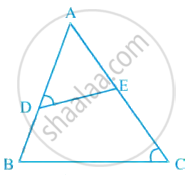
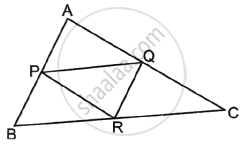
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
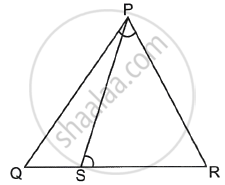
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.