Advertisements
Advertisements
Question
In the following figure, AB || QR. Find the length of PB.

Solution
We have, ΔPAB and ΔPQR
∠P = ∠P [common]
∠PAB = ∠PQR [corresponding angles]
Then, ΔPAB ~ ΔPQR [By AA similarity]
`therefore"PB"/"PR"="AB"/"QR"` [Corresponding parts of similar Δare proportional]
`rArr"PB"/6=3/9`
`rArr"PB"=3/9xx6=2` cm
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
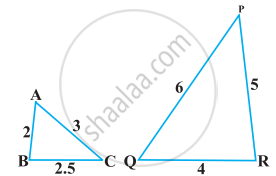
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
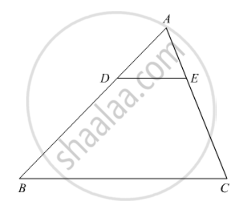
In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
The sides of certain triangles are given below. Determine which of them right triangles are.
1.4cm, 4.8cm, 5cm
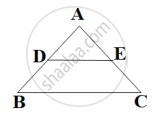
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
If ∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ∆ABC.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

