Advertisements
Advertisements
Question
In the following figure, XY || BC. Find the length of XY.
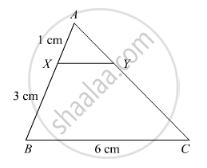
Solution
We have, XY || BC
In ΔAXY and ΔABC
∠A = ∠A [common]
∠AXY = ∠ABC [corresponding angles]
Then, ΔAXY ~ ΔABC [By AA similarity]
`therefore"AX"/"AB"="XY"/"BC"` [Corresponding parts of similar Δ are proportional]
`rArr1/4="XY"/6`
`rArr"XY"=6/4=1.5` cm
APPEARS IN
RELATED QUESTIONS
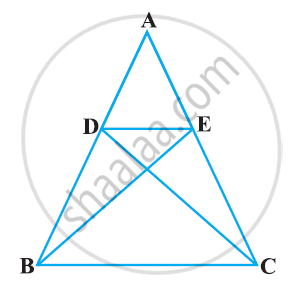
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?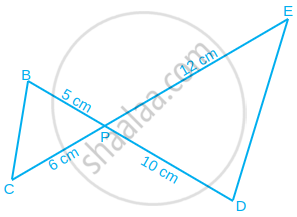
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.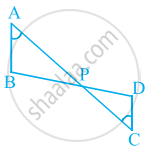
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

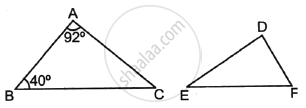
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
