Advertisements
Advertisements
Question
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?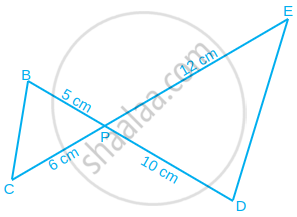
Solution
In ∆PBC and ∆PDE,
∠BPC = ∠EPD ...[Vertically opposite angles]
Now, `("PB")/("PD") = 5/10 = 1/2` ...(i)
And `("PC")/("PE") = 6/12 = 1/2` ...(ii)
From equations (i) and (ii),
`("PB")/("PD") = ("PC")/("PE")`
Since, one angle of ∆PBC is equal to one angle of ∆PDE and the sides including these angles are proportional, so both triangles are similar.
Hence, ∆PBC ~ ∆PDE, by SAS similarity criterion.
APPEARS IN
RELATED QUESTIONS
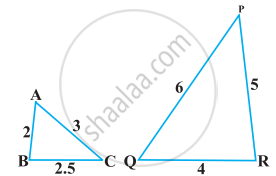
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
In the given figure MN|| BC and AM: MB= 1: 2
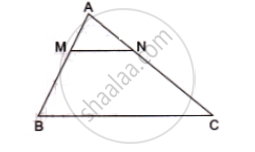
find ` (area(ΔAMN))/(area(ΔABC))`
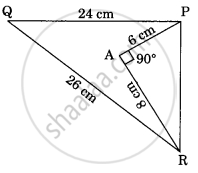
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.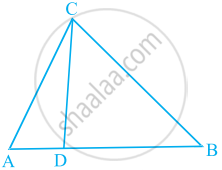
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?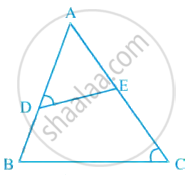
The sum of two angles of a triangle is 150°, and their difference is 30°. Find the angles.
