Advertisements
Advertisements
प्रश्न
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?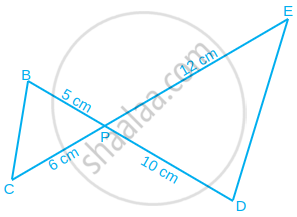
उत्तर
In ∆PBC and ∆PDE,
∠BPC = ∠EPD ...[Vertically opposite angles]
Now, `("PB")/("PD") = 5/10 = 1/2` ...(i)
And `("PC")/("PE") = 6/12 = 1/2` ...(ii)
From equations (i) and (ii),
`("PB")/("PD") = ("PC")/("PE")`
Since, one angle of ∆PBC is equal to one angle of ∆PDE and the sides including these angles are proportional, so both triangles are similar.
Hence, ∆PBC ~ ∆PDE, by SAS similarity criterion.
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
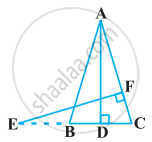
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).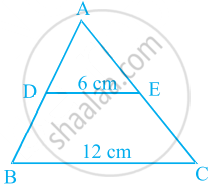
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

