Advertisements
Advertisements
प्रश्न
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
पर्याय
BC . EF = AC . FD
AB . EF = AC . DE
BC . DE = AB . EF
BC . DE = AB . FD
उत्तर
BC . DE = AB . EF
Explanation:
We know that,
If sides of one triangle are proportional to the side of the other triangle and the corresponding angles are also equal, then the triangles are similar by SSS similarity.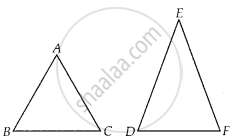
So, ∆ABC ∼ ∆EDF
Using similarity property,
`("AB")/("ED") = ("BC")/("DF") = ("AC")/("EF")`
Taking `("AB")/("ED") = ("BC")/("DF")`, we get
`("AB")/("ED") = ("BC")/("DF")`
AB . DF = ED . BC
So, option (d) BC . DE = AB . FD is true
Taking `("BC")/("DF") = ("AC")/("EF")`, we get
`("BC")/("DF") = ("AC")/("EF")`
⇒ BC . EF = AC . DF
So, option (a) BC . EF = AC . FD is true
Taking `("AB")/("ED") = ("AC")/("EF")`, we get,
`("AB")/("ED") = ("AC")/("EF")`
AB . EF = ED . AC
So, option (b) AB . EF = AC . DE is true.
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔABD ∼ ΔCBE
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower.
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
In figure, BD and CE intersect each other at the point P. Is ΔPBC ~ ΔPDE? Why?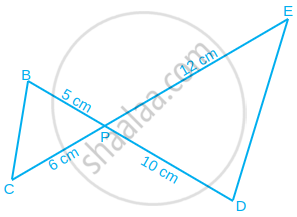
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

`square`ABCD is trapezium, AB || CD diagonals of trapezium intersects in point P.
Write the answers of the following questions:
- Draw the figure using the given information.
- Write any one pair of alternate angles and opposite angles.
- Write the names of similar triangles with the test of similarity.
