Advertisements
Advertisements
प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
उत्तर
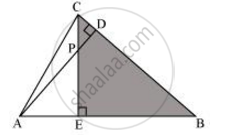
In ΔPDC and ΔBEC
∠PDC = ∠BEC = 90°
∠PCD = ∠BCE ...(Common angle)
Hence, by using the AA similarity criterion,
ΔPDC ∼ ΔBEC
संबंधित प्रश्न
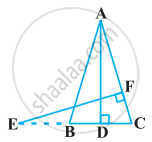
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
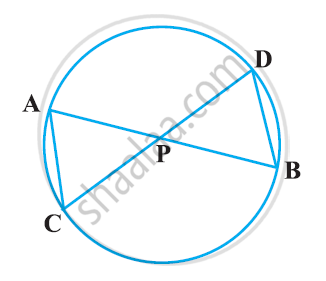
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
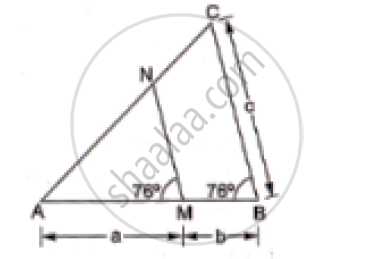
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
In the given figure, value of x(in cm) is

In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
In figure, if DE || BC, find the ratio of ar(ADE) and ar(DECB).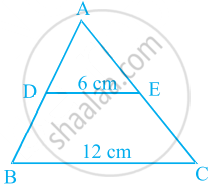
In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
In figure, if ∠D = ∠C, then it is true that ΔADE ~ ΔACB? Why?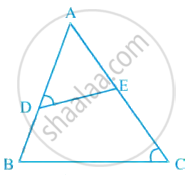
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.