Advertisements
Advertisements
प्रश्न
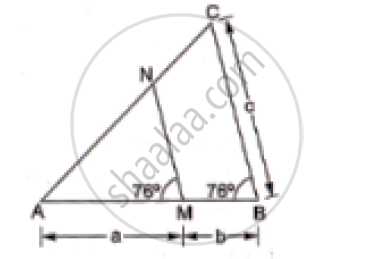
In the given figure, ∠AMN = ∠MBC = 76° . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.
उत्तर
Sol:
In ΔAMN and ΔABC
∠𝐴𝑀𝑁 = ∠𝐴𝐵𝐶 = 76° (𝐺𝑖𝑣𝑒𝑛)
∠𝐴 = ∠𝐴 (𝐶𝑜𝑚𝑚𝑜𝑛)
By AA similarity criterion, ΔAMN ~ ΔABC
If two triangles are similar, then the ratio of their corresponding sides are proportional
∴` (AM)/(AB)=(MN)/(BC)`
⇒ `(AM)/(AM+MB)=(MN)/(BC)`
⇒ `a/(a+b)=(MN)/c`
⇒ `MN=(ac)/(a+b)`
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
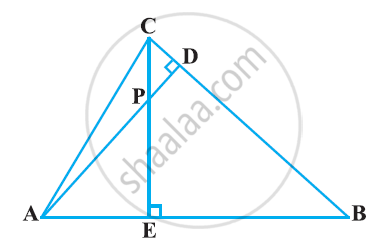
ΔAEP ∼ ΔADB
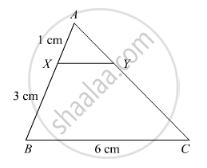
In the following figure, XY || BC. Find the length of XY.
In below figure, ∠A = ∠CED, Prove that ΔCAB ~ ΔCED. Also, find the value of x.
The sides of certain triangles are given below. Determine which of them right triangles are.
7cm, 24cm, 25cm
In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.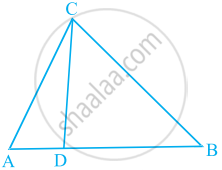
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

Which of the following is NOT a similarity criterion of traingles?
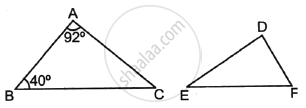
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?