Question

Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus. 

Answer 1

 

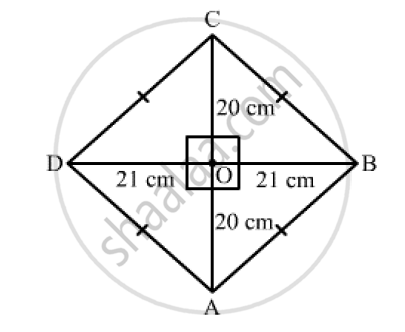
Suppose ABCD is a rhombus.
We know that the diagonals of a rhombus perpendicularly bisect each other.
∴ ∠𝐴𝑂𝐵 = 90°, 𝐴𝑂 = 20 𝑐𝑚 𝑎𝑛𝑑 𝐵𝑂 = 21 𝑐𝑚
Now, In right triangle AOB
By using Pythagoras theorem we have 

${\displaystyle A{B}^2=A{Q}^2+O{B}^2}$ 

=${\displaystyle {20}^2+{21}^2}$ 

=${\displaystyle 400+441}$ 

=${\displaystyle 841}$ 

∴ ${\displaystyle A{B}^2=841}$ 

⇒ ${\displaystyle AB=29cm}$ 

Since, all the sides of a rhombus are equal.
Hence, AB = BC = CD = DA = 29 cm