Advertisements
Advertisements
प्रश्न
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
उत्तर
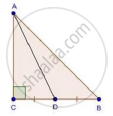
We have,
∠C = 90° and D is the mid-point of BC
In ΔACB, by Pythagoras theorem
AB2 = AC2 + BC2
⇒ AB2 = AC2 + (2CD)2 [D is the mid-point of BC]
AB2 = AC2 + 4CD2
⇒ AB2 = AC2 + 4(AD2 − AC2) [In ΔACD, by Pythagoras theorem]
⇒ AB2 = AC2 + 4AD2 − 4AC2
⇒ AB2 = 4AD2 − 3AC2
APPEARS IN
संबंधित प्रश्न
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus.
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `2sqrt(2)` then l (AB) = ?
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
Find the altitude of an equilateral triangle of side 8 cm.
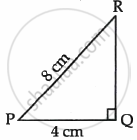
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.