Advertisements
Advertisements
प्रश्न
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
उत्तर
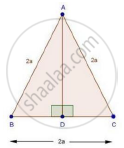
(i) In ΔABD and ΔACD
∠ADB = ∠ADC [Each 90°]
AB = AC [Given]
AD = AD [Common]
Then, ΔABD ≅ ΔACD [By RHS condition]
∴ BD = CD = a [By c.p.c.t]
In ΔADB, by Pythagoras theorem
AD2 + BD2 = AB2
⇒ AD2 + (a)2 = (2a)2
⇒ AD2 + a2 = 4a2
⇒ AD2 = 4a2 − a2 = 3a2
⇒ AD = a`sqrt3`
(ii) Area of ΔABC = `1/2xxBCxxAD`
`=1/2xx2axxasqrt3`
`=sqrt3` a2
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with sides BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
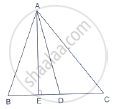
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
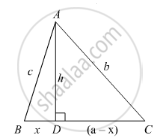
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
State Pythagoras theorem
In an equilateral triangle with side a, prove that area = `sqrt3/4` 𝑎2
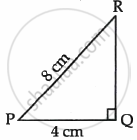
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.