Advertisements
Advertisements
प्रश्न
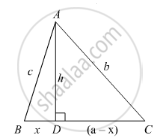
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
उत्तर
(i) Since AD perpendicular to BC we obtained two right angled triangles, triangle ADB and triangle ADC.
We will use Pythagoras theorem in the right angled triangle ADC
AC2 = AD2 + DC2 ......(1)
Let us substitute AD = h, AC = b and DC = (a − x) in equation (1) we get,
b2 = h2 + (a − x)2
b2 = h2 + a2 − 2ax + x2
b2 = h2 + a2 + 𝑥2 − 2ax ......(2)
(ii) Let us use Pythagoras theorem in the right angled triangle ADB as shown below,
AB2 = AD2 + BD2 ......(3)
Let us substitute AB = c, AD = h and BD = x in equation (3) we get,
c2 = h2 + x2
Let us rewrite the equation (2) as below,
b2 = h2 + x2 + a2 - 2ax ......(4)
Now we will substitute h2 + x2 = c2 in equation (4) we get,
b2 = c2 + a2 - 2ax
Therefore, b2 = c2 + a2 - 2ax.
APPEARS IN
संबंधित प्रश्न
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
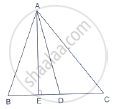
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
Find the altitude of an equilateral triangle of side 8 cm.
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
