Advertisements
Advertisements
प्रश्न
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
उत्तर
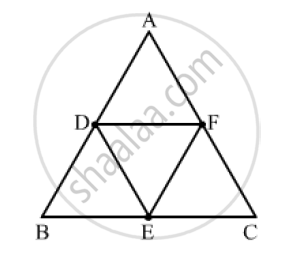
By using mid theorem i.e., the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.
∴ DF || BC
ANd `DF=1/2 BC`
⟹ DF = BE
Since, the opposite sides of the quadrilateral are parallel and equal.
Hence, BDFE is a parallelogram
Similarly, DFCE is a parallelogram.
Now, in ΔABC and ΔEFD
∠𝐴𝐵𝐶= ∠𝐸𝐹𝐷 (𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑎𝑛𝑔𝑙𝑒𝑠 𝑜𝑓 𝑎 𝑝𝑎𝑟𝑎𝑙𝑙𝑒𝑙𝑜𝑔𝑟𝑎𝑚)
∠𝐵𝐶𝐴=∠𝐸𝐷𝐹 (𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑎𝑛𝑔𝑙𝑒𝑠 𝑜𝑓 𝑎 𝑝𝑎𝑟𝑎𝑙𝑙𝑒𝑙𝑜𝑔𝑟𝑎𝑚)
By AA similarity criterion, ΔABC ~ ΔEFD
If two triangles are similar, then the ratio of their areas is equal to the squares of their corresponding sides.
∴ `(area(Δ DEF)) /(area(ΔABC))=((DF)/(BC))^2=((DF)/(2DF))^2=1/4`
Hence, the ratio of the areas of ΔDEF and ΔABC is 1 : 4.
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
A man goes 15 metres due west and then 8 metres due north. How far is he from the starting point?
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
State the converse of Pythagoras theorem.
The co-ordinates of the points A, B and C are (6, 3), (−3, 5) and (4, −2) respectively. P(x, y) is any point in the plane. Show that \[\frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \left| \frac{x + y - 2}{7} \right|\]
From given figure, In ∆ABC, AB ⊥ BC, AB = BC then m∠A = ?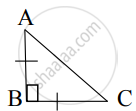
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?