Advertisements
Advertisements
प्रश्न
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
उत्तर
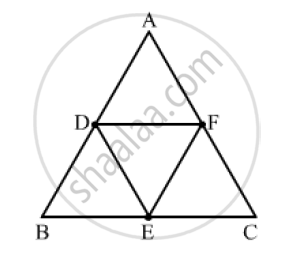
By using mid theorem i.e., the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.
∴ DF || BC
ANd `DF=1/2 BC`
⟹ DF = BE
Since, the opposite sides of the quadrilateral are parallel and equal.
Hence, BDFE is a parallelogram
Similarly, DFCE is a parallelogram.
Now, in ΔABC and ΔEFD
∠𝐴𝐵𝐶= ∠𝐸𝐹𝐷 (𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑎𝑛𝑔𝑙𝑒𝑠 𝑜𝑓 𝑎 𝑝𝑎𝑟𝑎𝑙𝑙𝑒𝑙𝑜𝑔𝑟𝑎𝑚)
∠𝐵𝐶𝐴=∠𝐸𝐷𝐹 (𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑎𝑛𝑔𝑙𝑒𝑠 𝑜𝑓 𝑎 𝑝𝑎𝑟𝑎𝑙𝑙𝑒𝑙𝑜𝑔𝑟𝑎𝑚)
By AA similarity criterion, ΔABC ~ ΔEFD
If two triangles are similar, then the ratio of their areas is equal to the squares of their corresponding sides.
∴ `(area(Δ DEF)) /(area(ΔABC))=((DF)/(BC))^2=((DF)/(2DF))^2=1/4`
Hence, the ratio of the areas of ΔDEF and ΔABC is 1 : 4.
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 1.6 cm, b = 3.8 cm and c = 4 cm
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
In an acute-angled triangle, express a median in terms of its sides.
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
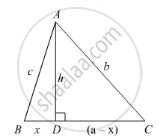
State Pythagoras theorem
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
