Advertisements
Advertisements
प्रश्न
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
उत्तर
Given: ∠CAB is an obtuse angle and P is the circumcentre of ΔABC.
Construction: Draw BD as diameter, join AD.
Proof: ∠CAD = ∠CBD ......[Angles on same arc]
⇒ ∠CAD = ∠CBP ......(i)
Also, ∠BAD = 90° ......(ii) [Angle in semi-circle]
Now, from figure,
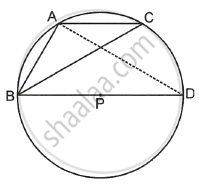
∠CAB = ∠CAD + ∠DAB
⇒ ∠CAB = ∠CBP + 90° ......[Using (i) and (ii)]
⇒ ∠CAB – ∠CBP = 90°
or ∠CAB – ∠PBC = 90°.
Hence proved.
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
In an equilateral ΔABC, AD ⊥ BC, prove that AD2 = 3BD2.
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
ΔABC~ΔDEF such that ar(ΔABC) = 64 cm2 and ar(ΔDEF) = `169cm^2`. If BC = 4cm, find EF.
Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
Find the height of an equilateral triangle having side 4 cm?
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
