Advertisements
Advertisements
प्रश्न
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
उत्तर
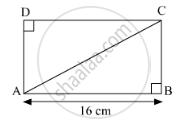
It is given that, area of rectangle is 192 sq.cm.
\[\text{Area} = \text{Length} \times \text{Breadth}\]
\[ \Rightarrow 192 = 16 \times \text{BC}\]
\[ \Rightarrow \text{BC} = \frac{192}{16}\]
\[ \Rightarrow \text{BC} = 12 \text{cm} . . . \left( 1 \right)\]
According to Pythagoras theorem,
In ∆ABC
\[{\text{AB}}^2 + {\text{BC}}^2 = {\text{AC}}^2 \]
\[ \Rightarrow \left( 16 \right)^2 + \left( 12 \right)^2 = {\text{AC}}^2 \]
\[ \Rightarrow 256 + 144 = {\text{AC}}^2 \]
\[ \Rightarrow {\text{AC}}^2 = 400\]
\[ \Rightarrow \text{AC} = 20 \text{cm}\]
Hence, the length of a diagonal of the rectangle is 20 cm.
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
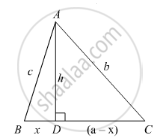
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
State Pythagoras theorem
State the converse of Pythagoras theorem.
Find the length of the altitude of an equilateral triangle of side 2a cm.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
Find the height of an equilateral triangle having side 4 cm?
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
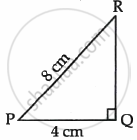
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.