Advertisements
Advertisements
प्रश्न
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
उत्तर
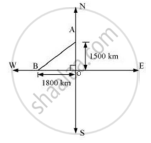
Distance traveled by the plane flying towards north in `1 1/2`hrs
`= 1000xx1 1/2=1500`km
Similarly, distance travelled by the plane flying towards west in `1 1/2`hrs
`=1200xx1 1/2=1800`km
Let these distances are represented by OA and OB respectively.
Now applying Pythagoras theorem
Distance between these planes after `1 1/2`hrs AB `=sqrt(OA^2+OB^2)`
`=sqrt(1500^2+1800^2)`
`=sqrt(2250000+3240000)`
`=sqrt5490000`
`=sqrt(9xx610000)`
`=300sqrt61`
So, distance between these planes will be `300sqrt61` km, after `1 1/2`hrs
APPEARS IN
संबंधित प्रश्न
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
State the converse of Pythagoras theorem.
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
ΔABC~ΔDEF such that ar(ΔABC) = 64 cm2 and ar(ΔDEF) = `169cm^2`. If BC = 4cm, find EF.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
From given figure, In ∆ABC, AB ⊥ BC, AB = BC then m∠A = ?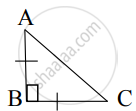
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `2sqrt(2)` then l (AB) = ?
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?