Advertisements
Advertisements
प्रश्न
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
उत्तर
It is given that ∆ABC is a right-angled at C and D is the mid-point of BC.

In the right angled triangle ADC, we will use Pythagoras theorem,
AD2 = DC2 + AC2 ..........(1)
Since D is the midpoint of BC, we have
`"DC"/="BC"/2`
Substituting `"DC"/="BC"/2` in equation (1), we get
`"AD"^2=("BC"/2)^2+"AC"^2`
`"AD"^2="BC"^2/4+"AC"^2`
4AD2 = BC2 + 4AC2
BC2 = 4AD2 - 4AC2
BC2 = 4(AD2 - AC2)
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:
(i) AB ✕ AQ = AC ✕ AP
(ii) BC2 = (AC ✕ CP + AB ✕ BQ)
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
In an equilateral triangle with side a, prove that area = `sqrt3/4` 𝑎2
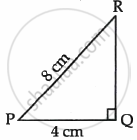
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.