Advertisements
Advertisements
प्रश्न
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
उत्तर
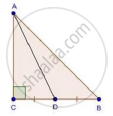
We have,
∠C = 90° and D is the mid-point of BC
In ΔACB, by Pythagoras theorem
AB2 = AC2 + BC2
⇒ AB2 = AC2 + (2CD)2 [D is the mid-point of BC]
AB2 = AC2 + 4CD2
⇒ AB2 = AC2 + 4(AD2 − AC2) [In ΔACD, by Pythagoras theorem]
⇒ AB2 = AC2 + 4AD2 − 4AC2
⇒ AB2 = 4AD2 − 3AC2
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with sides BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
In an acute-angled triangle, express a median in terms of its sides.
In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:
(i) AB ✕ AQ = AC ✕ AP
(ii) BC2 = (AC ✕ CP + AB ✕ BQ)
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus.
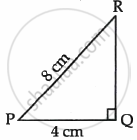
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.