Advertisements
Advertisements
प्रश्न
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
उत्तर
Let ABC be the Δ with
AB = (a – 1) cm BC = 2`sqrta` cm, CA = (a + 1) cm
Hence, AB2 = (a − 1)2 = a2 + 1 − 2𝑎
BC2 = (2`sqrta`)2 = 4a
CA2 = (a + 1)2 = a2 + 1 + 2a
Hence AB2 + BC2 = AC2
So Δ ABC is right angled Δ at B.
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
In an equilateral ΔABC, AD ⊥ BC, prove that AD2 = 3BD2.
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
From given figure, In ∆ABC, AB ⊥ BC, AB = BC then m∠A = ?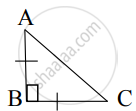
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
