Advertisements
Advertisements
प्रश्न
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
उत्तर
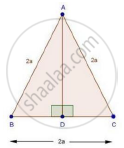
(i) In ΔABD and ΔACD
∠ADB = ∠ADC [Each 90°]
AB = AC [Given]
AD = AD [Common]
Then, ΔABD ≅ ΔACD [By RHS condition]
∴ BD = CD = a [By c.p.c.t]
In ΔADB, by Pythagoras theorem
AD2 + BD2 = AB2
⇒ AD2 + (a)2 = (2a)2
⇒ AD2 + a2 = 4a2
⇒ AD2 = 4a2 − a2 = 3a2
⇒ AD = a`sqrt3`
(ii) Area of ΔABC = `1/2xxBCxxAD`
`=1/2xx2axxasqrt3`
`=sqrt3` a2
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
In an acute-angled triangle, express a median in terms of its sides.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
The co-ordinates of the points A, B and C are (6, 3), (−3, 5) and (4, −2) respectively. P(x, y) is any point in the plane. Show that \[\frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \left| \frac{x + y - 2}{7} \right|\]
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
