Advertisements
Advertisements
प्रश्न
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
उत्तर
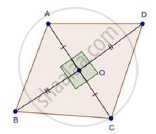
We have,
ABCD is a rhombus with diagonals AC = 10 cm and BD = 24 cm
We know that diagonal of a rhombus bisect each other at 90°
∴ AO = OC = 5 cm and BO = OD = 12 cm
In ΔAOB, by Pythagoras theorem
AB2 = AO2 + BO2
⇒ AB2 = 52 + 122
⇒ AB2 = 25 + 144 = 169
⇒ AB = `sqrt169` = 13 cm
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 8 cm, b = 10 cm and c = 6 cm
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
State the converse of Pythagoras theorem.
In an equilateral triangle with side a, prove that area = `sqrt3/4` 𝑎2
A man goes 12m due south and then 35m due west. How far is he from the starting point.
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
