Advertisements
Advertisements
प्रश्न
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
उत्तर
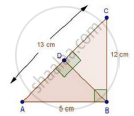
Let, AB = 5cm, BC = 12 cm and AC = 13 cm. Then, AC2 = AB2 + BC2. This proves that ΔABC is a right triangle, right angles at B. Let BD be the length of perpendicular from B on AC.
Now, Area ΔABC `=1/2(BCxxBA)`
`=1/2(12xx5)=30" cm"^2`
Also, Area of ΔABC `=1/2ACxxBD=1/2(13xxBD)`
`rArrBD=60/13`cm
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 8 cm, b = 10 cm and c = 6 cm
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
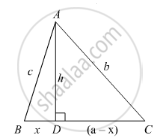
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:
(i) AB ✕ AQ = AC ✕ AP
(ii) BC2 = (AC ✕ CP + AB ✕ BQ)
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
In an equilateral triangle with side a, prove that area = `sqrt3/4` 𝑎2
The co-ordinates of the points A, B and C are (6, 3), (−3, 5) and (4, −2) respectively. P(x, y) is any point in the plane. Show that \[\frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \left| \frac{x + y - 2}{7} \right|\]
