Advertisements
Advertisements
प्रश्न
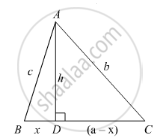
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
उत्तर
(i) Since AD perpendicular to BC we obtained two right angled triangles, triangle ADB and triangle ADC.
We will use Pythagoras theorem in the right angled triangle ADC
AC2 = AD2 + DC2 ......(1)
Let us substitute AD = h, AC = b and DC = (a − x) in equation (1) we get,
b2 = h2 + (a − x)2
b2 = h2 + a2 − 2ax + x2
b2 = h2 + a2 + 𝑥2 − 2ax ......(2)
(ii) Let us use Pythagoras theorem in the right angled triangle ADB as shown below,
AB2 = AD2 + BD2 ......(3)
Let us substitute AB = c, AD = h and BD = x in equation (3) we get,
c2 = h2 + x2
Let us rewrite the equation (2) as below,
b2 = h2 + x2 + a2 - 2ax ......(4)
Now we will substitute h2 + x2 = c2 in equation (4) we get,
b2 = c2 + a2 - 2ax
Therefore, b2 = c2 + a2 - 2ax.
APPEARS IN
संबंधित प्रश्न
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
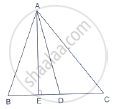
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
State the converse of Pythagoras theorem.
ΔABC~ΔDEF such that ar(ΔABC) = 64 cm2 and ar(ΔDEF) = `169cm^2`. If BC = 4cm, find EF.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `2sqrt(2)` then l (AB) = ?
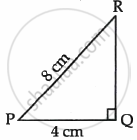
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.