Advertisements
Advertisements
Question
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
Solution
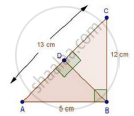
Let, AB = 5cm, BC = 12 cm and AC = 13 cm. Then, AC2 = AB2 + BC2. This proves that ΔABC is a right triangle, right angles at B. Let BD be the length of perpendicular from B on AC.
Now, Area ΔABC `=1/2(BCxxBA)`
`=1/2(12xx5)=30" cm"^2`
Also, Area of ΔABC `=1/2ACxxBD=1/2(13xxBD)`
`rArrBD=60/13`cm
APPEARS IN
RELATED QUESTIONS
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
In an acute-angled triangle, express a median in terms of its sides.
In an equilateral ΔABC, AD ⊥ BC, prove that AD2 = 3BD2.
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
State Pythagoras theorem
In an equilateral triangle with side a, prove that area = `sqrt3/4` 𝑎2
Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus.
From given figure, In ∆ABC, AB ⊥ BC, AB = BC then m∠A = ?