Advertisements
Advertisements
Question
In an equilateral triangle with side a, prove that area = `sqrt3/4` ๐2
Solution
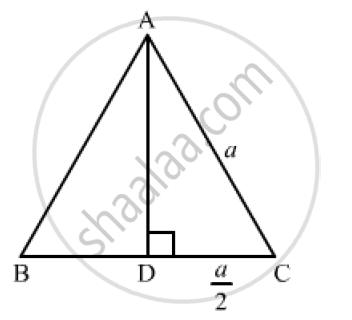
We know that the altitude of an equilateral triangle bisects the side on which it stands and forms right angled triangles with the remaining sides.
Suppose ABC is an equilateral triangle having AB =BC = CA = a.
Suppose AD is the altitude drawn from the vertex A to the side BC.
So, It will bisects the side BC
∴` DC=1/2 a `
Now, In right triangle ADC
By using Pythagoras theorem, we have
`AC^2=CD^2+DA^2`
⇒` a^2-(1/2 a)^2+DA^2`
⇒ `DA^2=a^2-1/4 a^2`
⇒` DA^2=3/4 a^2`
⇒`DA=sqrt3/2 a`
๐๐๐ค,๐๐๐๐ (Δ๐ด๐ต๐ถ)=`1/2xxBCxxAD`
=` 1/2xxaxxsqrt3/2 a`
=`sqrt3/4 a^2`
APPEARS IN
RELATED QUESTIONS
A man goes 15 metres due west and then 8 metres due north. How far is he from the starting point?
The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
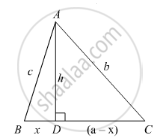
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
In an acute-angled triangle, express a median in terms of its sides.
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In โABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:
(i) AB โ AQ = AC โ AP
(ii) BC2 = (AC โ CP + AB โ BQ)
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
From given figure, In โABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of โAB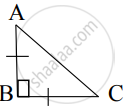C?
Find the height of an equilateral triangle having side 4 cm?
