Advertisements
Advertisements
Question
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Solution
Suppose ABCD is a rhombus.
We know that the diagonals of a rhombus perpendicularly bisect each other.
∴ ∠๐ด๐๐ต = `90^0` , ๐ด๐ = 12 ๐๐ ๐๐๐ ๐ต๐ = 5 ๐๐
Now, In right triangle AOB
By using Pythagoras theorem we have
`AB^2=AO^2+BO^2`
`=12^2+5^2`
`=144+25`
`=169`
∴` AB^2=169`
⇒ AB=13 cm
Since, all the sides of a rhombus are equal.
Hence, AB = BC = CD = DA = 13 cm
APPEARS IN
RELATED QUESTIONS
Construct a triangle ABC with sides BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are `3/4` times the corresponding sides of โABC.
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
ΔABC~ΔDEF such that ar(ΔABC) = 64 cm2 and ar(ΔDEF) = `169cm^2`. If BC = 4cm, find EF.
A man goes 12m due south and then 35m due west. How far is he from the starting point.
From given figure, In โABC, AB ⊥ BC, AB = BC then m∠A = ?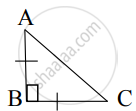
From given figure, In โABC, AB ⊥ BC, AB = BC, AC = `2sqrt(2)` then l (AB) = ?
