Advertisements
Advertisements
Question
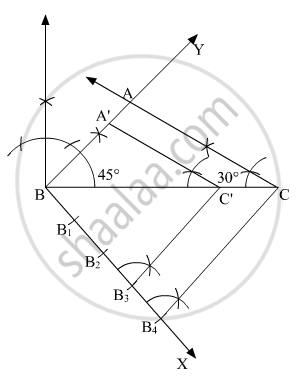
Construct a triangle ABC with sides BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
Solution
Steps of construction:
1. Draw line BC = 7 cm
2. At B, construct ∠CBY = 45° and at C, construct 180° −(105° + 45°) = 30°.
3. Mark the point of intersection of ∠B = 45° and ∠C = 30° as A. Thus, ∆ABC is obtained.
4. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
5. Locate 4 (3 < 4) points B1, B2, B3 and B4 on BX such that BB1 = B1B2 = B2B3 = B3B4.
6. Join B4C and draw a line through B3 parallel to B4C to intersect BC at C'.
7. Draw a line through C′ parallel to the line CA to intersect BA at A′
Then, ΔA′BC′ is the required triangle similar to the ΔABC
APPEARS IN
RELATED QUESTIONS
The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
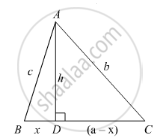
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In an equilateral triangle with side a, prove that area = `sqrt3/4` 𝑎2
A man goes 12m due south and then 35m due west. How far is he from the starting point.
The co-ordinates of the points A, B and C are (6, 3), (−3, 5) and (4, −2) respectively. P(x, y) is any point in the plane. Show that \[\frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \left| \frac{x + y - 2}{7} \right|\]
From given figure, In ∆ABC, AB ⊥ BC, AB = BC then m∠A = ?