Advertisements
Advertisements
Question
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Solution
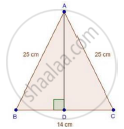
We have
AB = AC = 25 cm and BC = 14 cm
In ΔABD and ΔACD
∠ADB = ∠ADC [Each 90°]
AB = AC [Each 25 cm]
AD = AD [Common]
Then, ΔABD ≅ ΔACD [By RHS condition]
∴ BD = CD = 7 cm [By c.p.c.t]
In ΔADB, by Pythagoras theorem
AD2 + BD2 = AB2
⇒ AD2 + 72 = 252
⇒ AD2 = 625 − 49 = 576
⇒ AD = `sqrt576` = 24 cm
APPEARS IN
RELATED QUESTIONS
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 1.6 cm, b = 3.8 cm and c = 4 cm
A man goes 15 metres due west and then 8 metres due north. How far is he from the starting point?
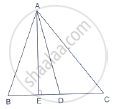
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
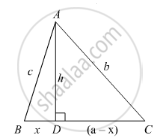
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
Find the length of the altitude of an equilateral triangle of side 2a cm.
ΔABC~ΔDEF such that ar(ΔABC) = 64 cm2 and ar(ΔDEF) = `169cm^2`. If BC = 4cm, find EF.
A man goes 12m due south and then 35m due west. How far is he from the starting point.
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
