Advertisements
Advertisements
Question
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?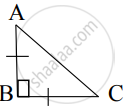
Solution
AB = BC ......[Given]
∴ ∠A = ∠C ......[Isosceles triangle theorem]
Let ∠A = ∠C = x ......(i)
In ∆ABC, ∠A + ∠B + ∠C = 180° ......[Sum of the measures of the angles of a triangle is 180°]
∴ x + 90° + x = 180° .......[From (i)]
∴ 2x = 90°
∴ x = `90^circ/2` .......[From (i)]
∴ x = 45°
∴ ∠A = ∠C = 45°
∴ ∆ABC is a 45° – 45° – 90° triangle.
∴ AB = BC = `1/sqrt(2) xx "AC"` ......[Side opposite to 45°]
= `1/sqrt(2) xx 5sqrt(2)`
∴ AB = BC = 5 units
∴ The height of ∆ABC is 5 units.
APPEARS IN
RELATED QUESTIONS
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 1.6 cm, b = 3.8 cm and c = 4 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 8 cm, b = 10 cm and c = 6 cm
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
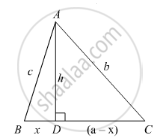
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
In an equilateral ΔABC, AD ⊥ BC, prove that AD2 = 3BD2.
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
State the converse of Pythagoras theorem.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
A man goes 12m due south and then 35m due west. How far is he from the starting point.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
