Advertisements
Advertisements
प्रश्न
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?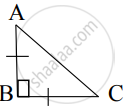
उत्तर
AB = BC ......[Given]
∴ ∠A = ∠C ......[Isosceles triangle theorem]
Let ∠A = ∠C = x ......(i)
In ∆ABC, ∠A + ∠B + ∠C = 180° ......[Sum of the measures of the angles of a triangle is 180°]
∴ x + 90° + x = 180° .......[From (i)]
∴ 2x = 90°
∴ x = `90^circ/2` .......[From (i)]
∴ x = 45°
∴ ∠A = ∠C = 45°
∴ ∆ABC is a 45° – 45° – 90° triangle.
∴ AB = BC = `1/sqrt(2) xx "AC"` ......[Side opposite to 45°]
= `1/sqrt(2) xx 5sqrt(2)`
∴ AB = BC = 5 units
∴ The height of ∆ABC is 5 units.
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 1.6 cm, b = 3.8 cm and c = 4 cm
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:
(i) AB ✕ AQ = AC ✕ AP
(ii) BC2 = (AC ✕ CP + AB ✕ BQ)
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
State Pythagoras theorem
State the converse of Pythagoras theorem.
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Find the length of the altitude of an equilateral triangle of side 2a cm.
In an equilateral triangle with side a, prove that area = `sqrt3/4` 𝑎2
Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus.
Find the altitude of an equilateral triangle of side 8 cm.
