Advertisements
Advertisements
प्रश्न
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
उत्तर
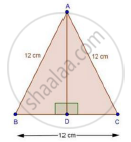
We have,
ΔABC is an equilateral Δ with side 12 cm.
Draw AE ⊥ BC
In ΔABD and ΔACD
∠ADB = ∠ADC [Each 90°]
AB = AC [Each 12 cm]
AD = AD [Common]
Then, ΔABD ≅ ΔACD [By RHS condition]
∴ AD2 + BD2 = AB2
⇒ AD2 + 62 = 122
⇒ AD2 = 144 − 36 = 108
⇒ AD = `sqrt`108 = 10.39 cm
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
In a ΔABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a`sqrt3`
(ii) Area (ΔABC) = `sqrt3` a2
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
ΔABC~ΔDEF such that ar(ΔABC) = 64 cm2 and ar(ΔDEF) = `169cm^2`. If BC = 4cm, find EF.
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
