Advertisements
Advertisements
प्रश्न
In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:
(i) AB ✕ AQ = AC ✕ AP
(ii) BC2 = (AC ✕ CP + AB ✕ BQ)
उत्तर
Given: ΔABC where ∠BAC is obtuse. PB ⊥AC and QC⊥AB.

To prove:
(i) AB × AQ = AC × AP and
(ii) BC2 = AC × CP + AB × BQ
Proof: In ΔACQ and ΔABP,
∠CAQ = ∠BAP (Vertically opposite angles)
∠Q = ∠P (= 90°)
∴ ΔACQ ∼ ΔABP [AA similarity test]
`rArr"CQ"/"BP"="AC"/"AB"="AQ"/"AP"` [Corresponding sides are in the same proportion]
`"AC"/"AB"="AQ"/"AP"`
⇒ AQ x AB = AC x AP .....(1)
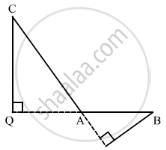
In right ΔBCQ,
⇒ BC2 = CQ2 + QB2
⇒ BC2 = CQ2 + (QA + AB)2
⇒ BC2 = CQ2 + QA2 + AB2 + 2QA × AB
⇒ BC2 = AC2 + AB2 + QA × AB + QA × AB [In right ΔACQ, CQ2 + QA2 = AC2]
⇒ BC2 = AC2 + AB2 + QA × AB + AC × AP (Using (1))
⇒ BC2 = AC (AC + AP) + AB (AB + QA)
⇒ BC2 = AC × CP + AB × BQ
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 8 cm, b = 10 cm and c = 6 cm
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
State the converse of Pythagoras theorem.
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `2sqrt(2)` then l (AB) = ?
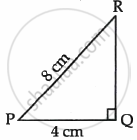
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.