Advertisements
Advertisements
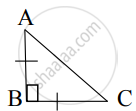
प्रश्न
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
उत्तर
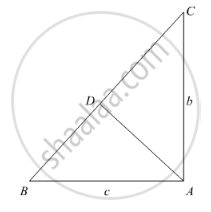
We have,
In ΔBAC, by Pythagoras theorem
BC2 = AB2 + AC2
⇒ BC2 = c2 + b2
⇒ BC = `sqrt(c^2+b^2)` ........(i)
In ΔABD and ΔCBA
∠B = ∠B [Common]
∠ADB = ∠BAC [Each 90°]
Then, ΔABD ~ ΔCBA [By AA similarity]
`therefore"AB"/"CB"="AD"/"CA"` [Corresponding parts of similar Δ are proportional]
`rArrc/sqrt(c^2+b^2)="AD"/b`
`rArr"AD"="bc"/sqrt(c^2+b^2)`
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
In an acute-angled triangle, express a median in terms of its sides.
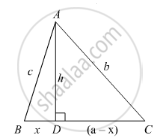
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
State Pythagoras theorem
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Find the length of the altitude of an equilateral triangle of side 2a cm.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
From given figure, In ∆ABC, AB ⊥ BC, AB = BC then m∠A = ?