Advertisements
Advertisements
प्रश्न
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
उत्तर
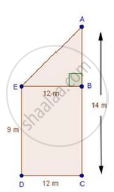
We have,
AC = 14 m, DC = 12m and ED = BC = 9m
Construction: Draw EB ⊥ AC
∴ AB = AC – BC = 14 – 9 = 5m
And, EB = DC = 12 m
In ΔABE, by Pythagoras theorem,
AE2 = AB2 + BE2
⇒ AE2 = 52 + 122
⇒ AE2 = 25 + 144 = 169
⇒ AE = `sqrt169` = 13 m
∴ Distance between their tops = 13 m
APPEARS IN
संबंधित प्रश्न
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
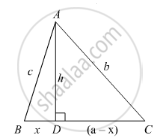
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
Find the height of an equilateral triangle having side 4 cm?
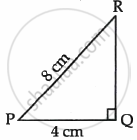
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.