Advertisements
Advertisements
प्रश्न
The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
उत्तर
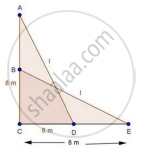
Let, length of ladder be AD = BE = `l` m
In ΔACD, by Pythagoras theorem
AD2 = AC2 + CD2
⇒ `l`2 = 82 + 62 .....(i)
In ΔBCE, by pythagoras theorem
BE2 = BC2 + CE2
⇒ `l`2 = BC2 + 82 .......(ii)
Compare (i) and (ii)
BC2 + 82 = 82 + 62
⇒ BC2 = 62
⇒ BC = 6m
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 8 cm, b = 10 cm and c = 6 cm
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
In an acute-angled triangle, express a median in terms of its sides.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
State Pythagoras theorem
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
