Advertisements
Advertisements
प्रश्न
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
उत्तर
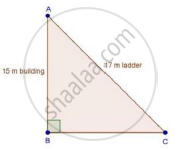
In ΔABC, by Pythagoras theorem
AB2 + BC2 = AC2
⇒ 152 + BC2 = 172
⇒ 225 + BC2 = 289
⇒ BC2 = 289 − 225
⇒ BC2 = 64
⇒ BC = 8 m
∴ Distance of the foot of the ladder from building = 8 m
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with sides BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
In an equilateral ΔABC, AD ⊥ BC, prove that AD2 = 3BD2.
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `2sqrt(2)` then l (AB) = ?
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?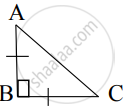
Find the height of an equilateral triangle having side 4 cm?
Find the altitude of an equilateral triangle of side 8 cm.
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
