Advertisements
Advertisements
प्रश्न
In an equilateral ΔABC, AD ⊥ BC, prove that AD2 = 3BD2.
उत्तर
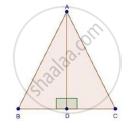
We have, ΔABC is an equilateral Δ and AD ⊥ BC
In ΔADB and ΔADC
∠ADB = ∠ADC [Each 90°]
AB = AC [Given]
AD = AD [Common]
Then, ΔADB ≅ ΔADC [By RHS condition]
∴ BD = CD =BC/2 .......(i) [corresponding parts of similar Δ are proportional]
In, ΔABD, by Pythagoras theorem
AB2 = AD2 + BD2
⇒ BC2 = AD2 + BD2 [AB = BC given]
⇒ [2BD]2 = AD2 + BD2 [From (i)]
⇒ 4BD2 − BD2 = AD2
⇒ 3BD2 = AD2
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with sides BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
State Pythagoras theorem
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?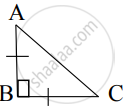
Find the height of an equilateral triangle having side 4 cm?
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
