Advertisements
Advertisements
प्रश्न
In an equilateral triangle with side a, prove that area = `sqrt3/4` 𝑎2
उत्तर
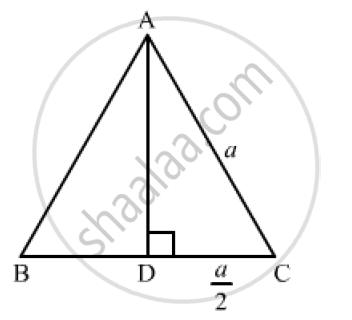
We know that the altitude of an equilateral triangle bisects the side on which it stands and forms right angled triangles with the remaining sides.
Suppose ABC is an equilateral triangle having AB =BC = CA = a.
Suppose AD is the altitude drawn from the vertex A to the side BC.
So, It will bisects the side BC
∴` DC=1/2 a `
Now, In right triangle ADC
By using Pythagoras theorem, we have
`AC^2=CD^2+DA^2`
⇒` a^2-(1/2 a)^2+DA^2`
⇒ `DA^2=a^2-1/4 a^2`
⇒` DA^2=3/4 a^2`
⇒`DA=sqrt3/2 a`
𝑁𝑜𝑤,𝑎𝑟𝑒𝑎 (Δ𝐴𝐵𝐶)=`1/2xxBCxxAD`
=` 1/2xxaxxsqrt3/2 a`
=`sqrt3/4 a^2`
APPEARS IN
संबंधित प्रश्न
A man goes 15 metres due west and then 8 metres due north. How far is he from the starting point?
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
The co-ordinates of the points A, B and C are (6, 3), (−3, 5) and (4, −2) respectively. P(x, y) is any point in the plane. Show that \[\frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \left| \frac{x + y - 2}{7} \right|\]
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `2sqrt(2)` then l (AB) = ?
Find the height of an equilateral triangle having side 4 cm?
Find the altitude of an equilateral triangle of side 8 cm.
