Advertisements
Advertisements
प्रश्न
The co-ordinates of the points A, B and C are (6, 3), (−3, 5) and (4, −2) respectively. P(x, y) is any point in the plane. Show that \[\frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \left| \frac{x + y - 2}{7} \right|\]
उत्तर
We know that the area of a triangle having vertices (x1, y1), (x2, y2) and (x3, y3) is\[\frac{1}{2}\left| x_1 \left( y_2 - y_3 \right) + x_2 \left( y_3 - y_1 \right) + x_3 \left( y_1 - y_2 \right) \right|\]
Area of ∆PBC
\[ = \frac{1}{2}\left| 7x + 7y - 14 \right|\]
\[ = \frac{7}{2}\left| x + y - 2 \right| \text{square units}\]
\[ = \frac{1}{2}\left| 42 + 15 - 8 \right|\]
\[ = \frac{49}{2} \text{square units}\]
\[ \Rightarrow \frac{ar\left( ∆ PBC \right)}{ar\left( ∆ ABC \right)} = \frac{\left| x + y - 2 \right|}{7} = \left| \frac{x + y - 2}{7} \right|\]
APPEARS IN
संबंधित प्रश्न
The sides of triangle is given below. Determine it is right triangle or not.
a = 7 cm, b = 24 cm and c = 25 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 8 cm, b = 10 cm and c = 6 cm
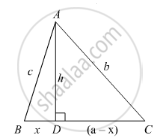
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
Find the length of the altitude of an equilateral triangle of side 2a cm.
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?