Advertisements
Advertisements
प्रश्न
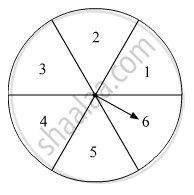
In fig. 7 is shown a disc on which a player spins an arrow twice. The fraction `a/b` is formed, where 'a' is the number of sector on which arrow stops on the first spin and 'b' is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction `a/b>1.`
उत्तर १
Elementary events associated with the experiment of spinning an arrow twice on a disc are
(1, 1), (1, 2), ...,(1, 6)
(2, 1), (2, 2), ...,(2, 6)
(3, 1), (3, 2), ...,(3, 6)
(4, 1), (4, 2), ...,(4, 6)
(5, 1), (5, 2), ...,(5, 6)
(6, 1), (6, 2), ...,(6, 6)
∴ Total number of elementary events = 36
It is given that a is the number of sector on which the arrow stops on the first spin and b is the number of the sector on which the arrow stops on the second spin.
Let A denote the event `a/b>1.`
Now,
`a/b>1Rightarrow a>b`
So, elementary events favourable to the event A are
(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4) and (6, 5)
∴ Total number of favourable events = 15
Thus,
Required probability =`"(The number of favourable events)"/"(Total number of the events)"=15/36 =5/12`
उत्तर २
Elementary events associated with the experiment of spinning an arrow twice on a disc are
(1, 1), (1, 2), ...,(1, 6)
(2, 1), (2, 2), ...,(2, 6)
(3, 1), (3, 2), ...,(3, 6)
(4, 1), (4, 2), ...,(4, 6)
(5, 1), (5, 2), ...,(5, 6)
(6, 1), (6, 2), ...,(6, 6)
∴ Total number of elementary events = 36
It is given that a is the number of sector on which the arrow stops on the first spin and b is the number of the sector on which the arrow stops on the second spin.
Let A denote the event `a/b>1.`
Now,
`a/b>1Rightarrow a>b`
So, elementary events favourable to the event A are
(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3), (6, 4) and (6, 5)
∴ Total number of favourable events = 15
Thus,
Required probability =`"(The number of favourable events)"/"(Total number of the events)"=15/36 =5/12`
APPEARS IN
संबंधित प्रश्न
Rahim tosses two different coins simultaneously. Find the probability of getting at least one tail.
All red face cards are removed from a pack of playing cards. The remaining cards were well shuffled and then a card is drawn at random from them. Find the probability that the drawn card is
(i) a red card
(ii) a face card
(iii) a card of clubs
Two dice are thrown together. The probability of getting the same number on both dice is.
A bag contains 3 red balls and 5 black balls. A ball is draw at random from the bag. What is the probability that the ball drawn is red?
All kings and queens are removed from a pack of 52 cards. The remaining cards are well shuffled and then a card is randomly drawn from it. Find the probability that this card is a red face card
Red queens and black jacks are removed from a pack of 52 playing cards. A card is drawn at random from the remaining cards, after reshuffling them. Find the probability that the card drawn is a queen
If a die is rolled, what is the probability that number appearing on upper face is less than 2?
A bag contains 4 white balls, 5 red balls, 2 black balls and 4 green balls. A ball is drawn at random from the bag. Find the probability that it is not green.
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the numbers 1, 2, 3,..., 12 as shown in the figure. What is the probability that it will point to a number which is a multiple of 5?
A lot consists of 144 ballpoint pens of which 20 are defective and others good. Tanvy will buy a pen if it is good, but will not buy it if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that she will buy it,
The probability of selecting a red ball at random from the jar that contains only red, blue and orange balls is `1/4`. The probability of selecting a blue ball at random from the same jar is `1/3`. If the jar contains 10 orange balls, find the total number of balls in the jar.
From a well-shuffled deck of 52 cards, one card is drawn at random. What is the probability of getting a queen?
One card is drawn at random from a well-shuffled deck of 52 cards. What is the probability of getting a 6?
A die is thrown once. Find the probability of getting a number which
lies between 2 and 6.
Three identical coins are tossed together. What is the probability of obtaining:
exactly one head?
Which of the following is not a random experiment?
A coin is tossed 12 times and the outcomes are observed as shown below:
The chance of occurrence of Head is
When a dice is thrown, outcomes 1, 2, 3, 4, 5, 6 are equally ______.
A dice is rolled once. What is the probability that the number on top will be odd
