Advertisements
Advertisements
प्रश्न
Find the area of the shaded region in Fig. 8, where \\

उत्तर
Area of the shaded region
= Area of the semicircle with diameter AD + Area of the semicircle with diameter BC
− Area of the semicircle with diameter AB − Area of the semicircle with diameter CD
\[= \frac{1}{2}\pi \left( \frac{14}{2} \right)^2 + \frac{1}{2}\pi \left( \frac{7}{2} \right)^2 - \frac{1}{2}\pi \left( \frac{3 . 5}{2} \right)^2 - \frac{1}{2}\pi \left( \frac{3 . 5}{2} \right)^2 \]
\[ = \frac{1}{2} \times \frac{22}{7} \times \left( \frac{3 . 5}{2} \right)^2 \times \left[ 16 + 4 - 1 - 1 \right]\]
\[ = \frac{1}{2} \times \frac{22}{7} \times \frac{3 . 5}{2} \times \frac{3 . 5}{2} \times 18\]
\[ = 86 . 625 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
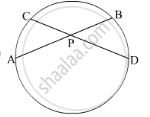
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
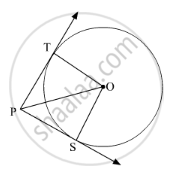
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
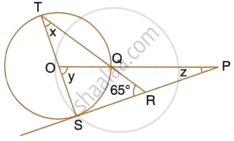
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
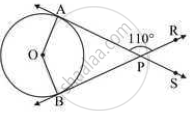
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The number of tangents drawn at a point of the circle is/are ______
The angle between two tangents to a circle may be 0°.
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
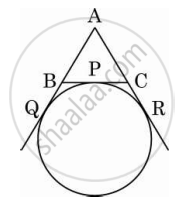
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

