Advertisements
Advertisements
प्रश्न
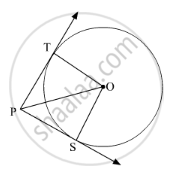
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
उत्तर
It is given that PS and PT are tangents to the circle with centre O. Also, ∠SPT = 120°.
To prove: OP = 2PS
Proof: \[In ∆ PTO\ and ∆ PSO,\]
PT = PS (Tangents drawn from an external point to a circle are equal in length.)
TO = SO (Radii of the circle)
∠PTO = ∠PSO = \[90^o\]
Thus,
∠TPO = ∠SPO =\[\frac{120^o}{2} = 60^o\]
Now, in \[∆ PSO,\]
\[\cos60^o = \frac{PS}{PO}\]
\[ \Rightarrow \frac{1}{2} = \frac{PS}{PO}\]
\[ \Rightarrow PO = 2PS\]
APPEARS IN
संबंधित प्रश्न
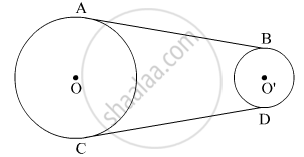
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
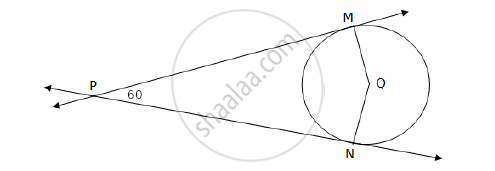
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The length of the tangent from an external point P on a circle with centre O is ______
The length of the tangent from an external point on a circle is ______
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
The angle between two tangents to a circle may be 0°.
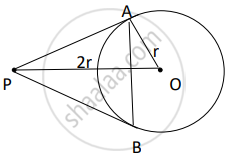
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?