Advertisements
Advertisements
प्रश्न
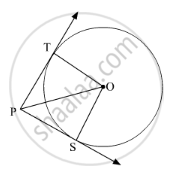
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
उत्तर
It is given that PS and PT are tangents to the circle with centre O. Also, ∠SPT = 120°.
To prove: OP = 2PS
Proof: \[In ∆ PTO\ and ∆ PSO,\]
PT = PS (Tangents drawn from an external point to a circle are equal in length.)
TO = SO (Radii of the circle)
∠PTO = ∠PSO = \[90^o\]
Thus,
∠TPO = ∠SPO =\[\frac{120^o}{2} = 60^o\]
Now, in \[∆ PSO,\]
\[\cos60^o = \frac{PS}{PO}\]
\[ \Rightarrow \frac{1}{2} = \frac{PS}{PO}\]
\[ \Rightarrow PO = 2PS\]
APPEARS IN
संबंधित प्रश्न
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
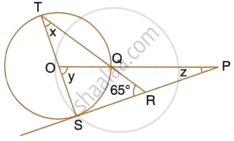
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
The length of the tangent from an external point on a circle is ______
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
